データ解析のための統計モデリング入門 マルコフ連鎖モンテカルロ(MCMC)法とベイズ統計モデル 読書メモ3

このブログ記事は『データ解析のための統計モデリング入門』（久保拓弥　著、岩波書店）という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。 今回は第８章、マルコフ連鎖モンテカルロ(MCMC)法とベイズ統計モデルについてのまとめの三回目です。 この章ではMCMCやメトロポリス法について説明がされています。 その中で、メトロポリス法によるサンプリングが解説されています。 なので、同じようにメトロポリス法でサンプリングしてみるコードを用意しました。 コードはRで書きました。

dataSize <- 20
N <- 8

data <- rbinom(dataSize, N, 0.45)

likelihood <- function (q) {
sum(log(dbinom(data, N, q)))
}

develop <- function(q) {
if (runif(1, 0, 1) < 0.5) {
q + 0.01
} else {
q - 0.01
}
}

sampling <- function(n, init) {
q <- init
ql <- likelihood(q)
samples <- vector(length = n)
i <- 1
while(i <= n) {
p <- develop(q)
pl <- likelihood(p)
r <- log(runif(1, 0, 1))
if (ql < pl || r < pl - ql) {
q <- p
ql <- pl
}
samples[i] <- p
i <- i + 1
}
samples
}

samples1 <- sampling(500, 0.3)
hist(samples1, breaks = seq(0, 1, by = 0.01), main = "500 samples", xlab = "q")

samples2 <- c(samples1, sampling(500, samples1[500]))
hist(samples2, breaks = seq(0, 1, by = 0.01), main = "1000 samples", xlab = "q")

samples3 <- c(samples2, sampling(1000, samples2[1000]))
hist(samples3, breaks = seq(0, 1, by = 0.01), main = "2000 samples", xlab = "q")

samples4 <- c(samples3, sampling(8000, samples3[2000]))
hist(samples4, breaks = seq(0, 1, by = 0.01), main = "10000 samples", xlab = "q")

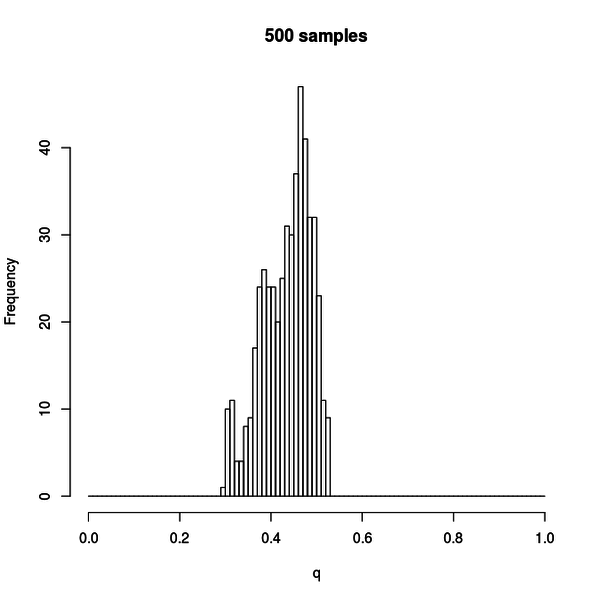
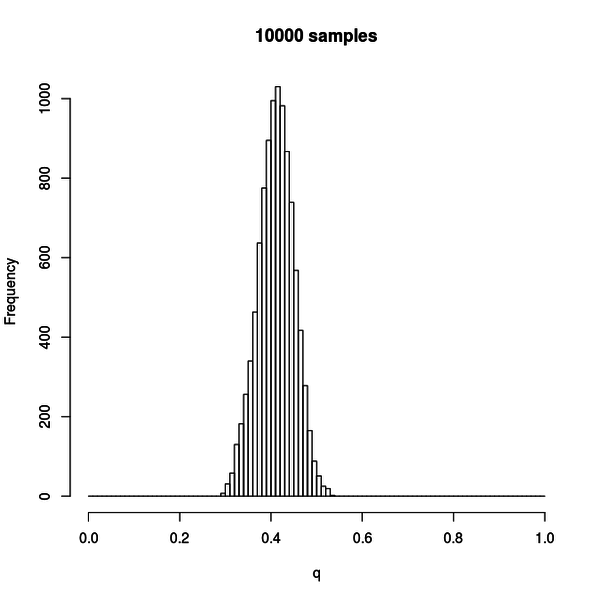
サンプルデータとしては、本の中でやっているのと同じように、事象の発生確率が `0.45` で、事象の試行回数は `8` の二項分布から、`20` 個のサンプルを取って用意しました。 なので、このデータに対して `q` のサンプリングをすると、だいたい `0.45` を中心とした分布が得られるはずです。 コードではサンプル数が `500`、 `1000`、 `2000`、 `10000` の時にヒストグラムをプロットしています。 コードを実行すると次のような図がプロットされます。 この図はサンプル数 `500` の場合です。 まだヒストグラムが凸凹しているのが分かります。 この図はサンプル数 `10000` の場合です。 だいぶヒストグラムがなめらかになって、分布が収束してきているのが分かります。