前回、偏微分方程式の数値解の結果を示したが、これをどうやって計算したかについて説明していこうと思う。
まず、対象とする一辺Lの正方形領域をメッシュに切ろう。頂点がN*N個になるように切って計算したのが前回の図である。すると、格子の一辺の長さΔはL/(N-1)なのだが、そんなものは全体に共通なので係数を掛けたり割ったりだけに過ぎず本質的でないので、格子の一辺の長さは1としよう。これで計算が楽になる。
次に、2次のポアソンの偏微分はどうすれば計算できるかを考える。微分、偏微分では、隣の点との差分を計算すればよく、2階編微分になっているので、差分の差分をとれば大丈夫ということで、次図のイメージで計算すればよいと思われる。
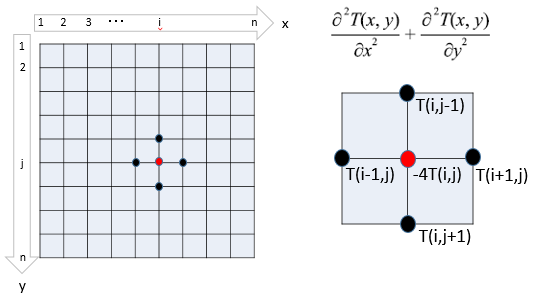 ところで、上図の各格子点に対して、上下左右の隣点の値(温度)の和から対象点(i,j)の値(温度)の4倍を引けば2階編微分に相当する値が出るはずである。今回は、この値が0で、方程式が格子点(i,j)に対して1つ出来上がる。
ところで、上図の各格子点に対して、上下左右の隣点の値(温度)の和から対象点(i,j)の値(温度)の4倍を引けば2階編微分に相当する値が出るはずである。今回は、この値が0で、方程式が格子点(i,j)に対して1つ出来上がる。
そして、こういう点がn*n個あるので、方程式の数がn*n個と膨大になる。全ての格子点の温度T(i,j)が変数なので、変数の数がn*n個。そして、方程式の数がn*n個だと、これはn*n元の連立一次方程式になり解けるはずなのだ。
係数行列をCとすると、Cはサイズn*nの正方行列になるわけで、格子点(i,j)に対する式は、i+(j-1)*n 行目の係数で表される。この点については、どういう風に計算するかの説明が必要なのだが、境界条件の説明するときに合わせて行う。
この係数行列は規則的なので作ろうと思えば作れるのだが、Octaveは非常に多数の便利な行列を自動生成してくれる機能があり、そのための関数がgallery()である。
第1引数に、行列の種類を文字列で指定する。”poisson”のとき、第2引数に元の分割数n(4)を指定すると、サイズがn*n(16)の正方行列が作られる。
full()は、gallary()が出力する行列がスパースな行列なので、そのまま表示すると、0以外が入っている箇所しか示さないので、普通の行列に展開するために使った。よく使われる行列の多くは、ほとんどの要素が0というのが多く、値の入っているところだけデータを持つことで、メモリが非常に圧縮できるし、計算も早くなったりする。
最初の図に従うと、点(i,j)の係数は-4で、隣の点は1でなければいけないのだが、この行列は符号が逆転している。でも、どうせ偏微分の結果は0なのだから、符合が逆転しても結果は同じになるので、このまま使ってしまおう。
配列は大きくなると、一覧性がどんどん悪くなる。それで、配列の状態を一瞬で把握できるような関数も用意されている。
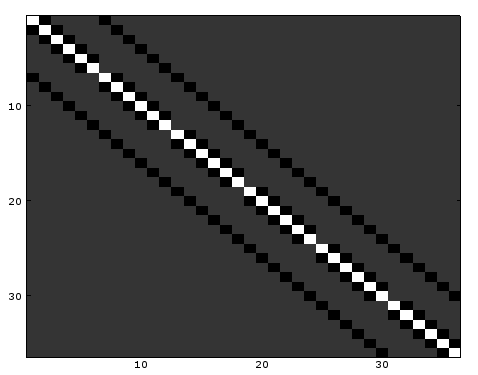
6×6の格子点に対するポアソンの行列なので、36次の正方行列になった。
対角線の白マスが4を示し、グレイが0、黒が-1になっている。
上下左右の4点を指定しようとしても、外周上の格子点の場合、4つの隣点のうちの少なくとも1つは存在しない点になるため、横の行を見ると、黒が本来4箇所ないといけないのだが、3箇所や2箇所になっている場所がある。これは境界に対して発生しているわけである。
さて、境界の問題が出てきたが、そもそもポアソンの方程式、解こうと思ったら何らかの条件が必要になる。今回は、外周上の格子点の温度を指定することで解く。
このような境界条件を指定しなければいけないのだが、それに合わせて、得られた行列も調整する必要があるのだが、それは次に説明視よう。
まず、対象とする一辺Lの正方形領域をメッシュに切ろう。頂点がN*N個になるように切って計算したのが前回の図である。すると、格子の一辺の長さΔはL/(N-1)なのだが、そんなものは全体に共通なので係数を掛けたり割ったりだけに過ぎず本質的でないので、格子の一辺の長さは1としよう。これで計算が楽になる。
次に、2次のポアソンの偏微分はどうすれば計算できるかを考える。微分、偏微分では、隣の点との差分を計算すればよく、2階編微分になっているので、差分の差分をとれば大丈夫ということで、次図のイメージで計算すればよいと思われる。
 ところで、上図の各格子点に対して、上下左右の隣点の値(温度)の和から対象点(i,j)の値(温度)の4倍を引けば2階編微分に相当する値が出るはずである。今回は、この値が0で、方程式が格子点(i,j)に対して1つ出来上がる。
ところで、上図の各格子点に対して、上下左右の隣点の値(温度)の和から対象点(i,j)の値(温度)の4倍を引けば2階編微分に相当する値が出るはずである。今回は、この値が0で、方程式が格子点(i,j)に対して1つ出来上がる。そして、こういう点がn*n個あるので、方程式の数がn*n個と膨大になる。全ての格子点の温度T(i,j)が変数なので、変数の数がn*n個。そして、方程式の数がn*n個だと、これはn*n元の連立一次方程式になり解けるはずなのだ。
係数行列をCとすると、Cはサイズn*nの正方行列になるわけで、格子点(i,j)に対する式は、i+(j-1)*n 行目の係数で表される。この点については、どういう風に計算するかの説明が必要なのだが、境界条件の説明するときに合わせて行う。
この係数行列は規則的なので作ろうと思えば作れるのだが、Octaveは非常に多数の便利な行列を自動生成してくれる機能があり、そのための関数がgallery()である。
>> full(gallery("poisson",4))
ans =
4 -1 0 0 -1 0 0 0 0 0 0 0 0 0 0 0
-1 4 -1 0 0 -1 0 0 0 0 0 0 0 0 0 0
0 -1 4 -1 0 0 -1 0 0 0 0 0 0 0 0 0
0 0 -1 4 0 0 0 -1 0 0 0 0 0 0 0 0
-1 0 0 0 4 -1 0 0 -1 0 0 0 0 0 0 0
0 -1 0 0 -1 4 -1 0 0 -1 0 0 0 0 0 0
0 0 -1 0 0 -1 4 -1 0 0 -1 0 0 0 0 0
0 0 0 -1 0 0 -1 4 0 0 0 -1 0 0 0 0
0 0 0 0 -1 0 0 0 4 -1 0 0 -1 0 0 0
0 0 0 0 0 -1 0 0 -1 4 -1 0 0 -1 0 0
0 0 0 0 0 0 -1 0 0 -1 4 -1 0 0 -1 0
0 0 0 0 0 0 0 -1 0 0 -1 4 0 0 0 -1
0 0 0 0 0 0 0 0 -1 0 0 0 4 -1 0 0
0 0 0 0 0 0 0 0 0 -1 0 0 -1 4 -1 0
0 0 0 0 0 0 0 0 0 0 -1 0 0 -1 4 -1
0 0 0 0 0 0 0 0 0 0 0 -1 0 0 -1 4
第1引数に、行列の種類を文字列で指定する。”poisson”のとき、第2引数に元の分割数n(4)を指定すると、サイズがn*n(16)の正方行列が作られる。
full()は、gallary()が出力する行列がスパースな行列なので、そのまま表示すると、0以外が入っている箇所しか示さないので、普通の行列に展開するために使った。よく使われる行列の多くは、ほとんどの要素が0というのが多く、値の入っているところだけデータを持つことで、メモリが非常に圧縮できるし、計算も早くなったりする。
最初の図に従うと、点(i,j)の係数は-4で、隣の点は1でなければいけないのだが、この行列は符号が逆転している。でも、どうせ偏微分の結果は0なのだから、符合が逆転しても結果は同じになるので、このまま使ってしまおう。
配列は大きくなると、一覧性がどんどん悪くなる。それで、配列の状態を一瞬で把握できるような関数も用意されている。
>> colormap("gray")
>> imagesc(full(gallery("poisson",6)))

6×6の格子点に対するポアソンの行列なので、36次の正方行列になった。
対角線の白マスが4を示し、グレイが0、黒が-1になっている。
上下左右の4点を指定しようとしても、外周上の格子点の場合、4つの隣点のうちの少なくとも1つは存在しない点になるため、横の行を見ると、黒が本来4箇所ないといけないのだが、3箇所や2箇所になっている場所がある。これは境界に対して発生しているわけである。
さて、境界の問題が出てきたが、そもそもポアソンの方程式、解こうと思ったら何らかの条件が必要になる。今回は、外周上の格子点の温度を指定することで解く。
このような境界条件を指定しなければいけないのだが、それに合わせて、得られた行列も調整する必要があるのだが、それは次に説明視よう。
ここでは、非常に足早に必要なことも省略しながら説明しているので、この分野の計算についてちゃんと知りたい場合は、「偏微分方程式の数値解法」などのキーワードでググってみよう。あちこちの大学の講義資料や書籍がみつかるので、それらできちんと勉強しよう。



