通常の巡回セールスマン問題は、スタート地点まで戻る、つまり一周する最短のループを求めるのであるが、それとはちょっと違う次図の場合について考えてみよう。
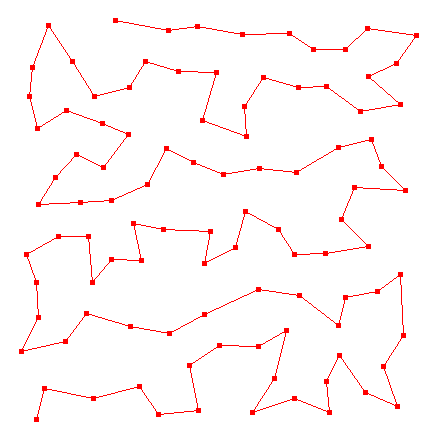
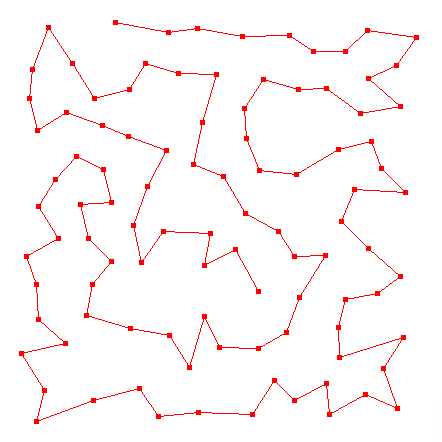
全ての点を結んでいるが、元の点には戻っていない。こういう場合の最短経路が欲しい場合もあろう。
開始点、終了点を任意としているので、実行の度に異なる。
求まるのは準最適解(それなりに良い解)であり、理論上の最適解ではないので、実行毎に異なってしまう。
さて、どうプログラムを変更すれば良いだろうか?
実は、非常に簡単である。
N点の順番が決まったら、1周する場合は、最後から最初への距離もfitness関数(全道程)に加えていたのだが、それ止めただけである。
また、表示も、最後から開始点への線を結ぶのを止めただけである。
簡単なので、それ以上の説明は不要だろう。
さて、今回頭に入れておくべきことは、巡回セールス問題は、1周しないバージョンも可能ということ。
そもそも、N点を並べた時に、最後の次の点を最初の点にして1周したことにしていた方が小細工を施していたと言えよう。
そう考えると、巡回セールスマン問題のアルゴリズムは、N個の順列がベースとなる問題に適応できることがわかる。
つまり、1周しない問題にも、ほぼそのまま適応できるということである。



